[LeetCode] 1220. Count Vowels Permutation

2022-05-27 23:58:26 #编程
This post is also available in English and alternative languages.

题目大意

  • 定义字符集 a, e, i, o, u
  • 定义字符连接规则
    • Each vowel a may only be followed by an e.
    • Each vowel e may only be followed by an a or an i.
    • Each vowel i may not be followed by another i.
    • Each vowel o may only be followed by an i or a u.
    • Each vowel u may only be followed by an a.
  • 结果对 $10^9 + 7$ 取模
  • 取值范围：$1 <= n <= 2 * 10^4$

问：对于给定的长度 $n$，存在多少种不同的字符串排列？

分析

根据题意可以绘出一个有向图。

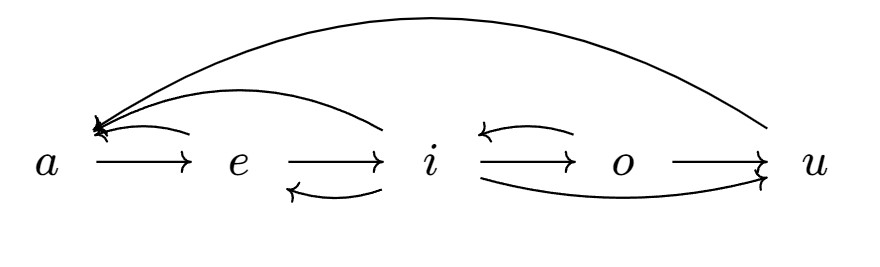
计算得出各节点的出度和入度。

1
2
3
4
5
6
7
8
// outdegree
{
    "a": 1,
    "e": 2,
    "i": 4,
    "o": 2,
    "u": 1
}
1
2
3
4
5
6
7
8
// indegree
{
    "a": 3,
    "e": 2,
    "i": 2,
    "o": 1,
    "u": 2
}
  • 已知样例 $n$ 取值 1, 2, 5 时答案分别为 5, 10, 68。因为结果需要对大素数取模，而数据取值范围并不大，所以说明答案呈指数级增长。

求解

笔试时很不幸地抽中这道 hard 难度的 DP 题，没能写出来。事后发现当作模拟题来写其实也行，从 $n=1$ 的状态向上依次计算即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def countVowelPermutation(self, n: int) -> int:
    keys = ['a', 'e', 'i', 'o', 'u']
    s = {'a': 1, 'e': 1, 'i': 1, 'o': 1, 'u': 1}
    d1 = {
        'a': 1,
        'e': 2,
        'i': 4,
        'o': 2,
        'u': 1
    }
    d2 = {
        'a': ['e'],
        'e': ['a', 'i'],
        'i': ['a', 'e', 'o', 'u'],
        'o': ['i', 'u'],
        'u': ['a']
    }
    res = 5
    for i in range(n - 1):
        res = 0
        for k in keys:
            res += s[k] * d1[k]
        t = {k: 0 for k in keys}
        for k in keys:
            for k2 in d2[k]:
                t[k2] += s[k] % 1000000007
        s = t
    return res % 1000000007

至于 DP 的标准解法，关键在于得出状态转移方程。从前序状态的值计算得到当前状态值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// https://github.com/grandyang/leetcode/issues/1220
int countVowelPermutation(int n) {
    int res = 0, M = 1e9 + 7;
    vector<char> vowels{'a', 'e', 'i', 'o', 'u'};
    vector<vector<long>> dp(n, vector<long>(5));

    for (int j = 0; j < 5; ++j)
        dp[0][j] = 1;

    for (int i = 1; i < n; ++i) {
        // 状态转移方程，对应每个字符的 indegree
        dp[i][0] = (dp[i - 1][1] + dp[i - 1][2] + dp[i - 1][4]) % M;
        dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % M;
        dp[i][2] = (dp[i - 1][1] + dp[i - 1][3]) % M;
        dp[i][3] = dp[i - 1][2];
        dp[i][4] = (dp[i - 1][2] + dp[i - 1][3]) % M;
    }

    for (int j = 0; j < 5; ++j)
        res = (res + dp[n - 1][j]) % M;

    return res;
}
Prev
2022-05-27 23:58:26 #编程
Next